上一次说到选特征的一个简单方法, 但是如果真的要评估一个方法或者一类特征的效果, 简单的相似度计算是不够的, 在上线实验之前, 还是需要有一些别的方式来做验证.

我遇到过的大部分机器学习问题, 最终都转成了二分类问题 (概率问题). 最直白的比如 A 是否属于集合 S (某照片中的人脸是否是人物 Z), 排序问题也可以转换为二分类问题, 比如广告点击率或推荐的相关度, 把候选集分为点击/不点击或接受推荐/不接受推荐的二分类概率. 那在上线之前, 可以用过一些分类器性能评估的方法来做离线评估.

分类器的正确率和召回率

前几天在无觅上看到有人分享了一篇 数据不平衡时分类器性能评价之ROC曲线分析, 把这个问题已经讲差不多了, 我这复述一下.

先说混淆矩阵 (confusion matrix). 混淆矩阵是评估分类器可信度的一个基本工具, 设实际的所有正样本为 P (real-Positive), 负样本为 N (real-Negative), 分类器分到的正样本标为 pre-Positive’, 负样本标为 pre-Negetive’, 则可以用下面的混淆矩阵表示所有情况:

              | real-positive       | real-negative
pre-positive' | TP (true positive)  | FP (false positive)
pre-negative' | FN (false negative) | TN (true negative)

通过这个矩阵, 可以得到很多评估指标:

FP rate = FP / N
TP rate = TP / P
Accuracy = (TP + TN) / (P + N)    # 一般称之为准确性或正确性
Precision = TP / (TP + FP)        # 另一些领域的准确性或正确性, 经常需要看上下文来判断
Recall = TP / P                   # 一般称之为召回率
F-score = Precision * Recall

在我接触过的大部分工作中, 大家都在关注 Precision 和 Recall. 同引用原文中提到的, 这样的分类评估性能只在数据比较平衡时比较好用 (正负例比例接近), 在很多特定情况下正负例是明显有偏的 (比如万分之几点击率的显示广告), 那就只能作为一定的参考指标.

分类器的排序能力评估

很多情况下我们除了希望分类器按某个阈值将正负样本完全分开, 同时还想知道候选集中不同条目的序关系. 比如广告和推荐, 首先需要一个基础阈值来保证召回的内容都满足基本相关度, 比如我一大老爷们去搜笔记本维修代理你给我出一少女睫毛膏的广告或推荐关注, 我绝对飙一句你大爷的然后开 AdBlock 屏蔽之. 在保证了基础相关性 (即分类器的正负例分开) 后, 则需要比较同样是正例的集合里, 哪些更正点 (其实说白了就是怎样才收益最大化). 一般来说, 如果分类器的输出是一个正例概率, 则直接按这个概率来排序就行了. 如果最终收益还要通过评估函数转换, 比如广告的 eCPM = CTR*Price, 或推荐里 rev = f(CTR), (f(x) 是一个不同条目的获益权重函数), 那么为了评估序是否好, 一般会再引入 ROC 曲线和 AUC 面积两个指标.

ROC 曲线全称是 Receiver Operating Characteristic (ROC curve), 详细的解释可以见维基百科上的英文词条 Receiver_operating_characteristic 或中文词条 ROC曲线. 我对 ROC 曲线的理解是, 对某个样本集, 当前分类器对其分类结果的 FPR 在 x 时, TPR 能到 y. 如果分类器完全准确, 则在 x = 0 时 y 就能到 1, 如果分类器完全不靠谱, 则在 x = 1 时 y 还是为 0, 如果 x = y, 那说明这个分类器在随机分类. 因为两个都是 Rate, 是 [0, 1] 之间的取值, 所以按此方法描的点都在一个 (0, 0), (1, 1) 的矩形内, 拉一条直线从 (0, 0) 到 (1, 1), 如果描点在这条直线上, 说明分类器对当前样本就是随机分的 (做分类最悲催的事), 如果描点在左上方, 说明当前分类器对此样本分类效果好过随机, 如果在右下方, 那说明分类器在做比随机还坑爹的反向分类. 引用维基百科上的一个图来说明:

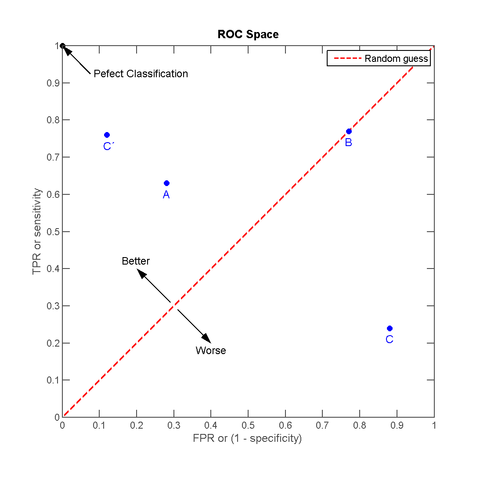
其中 C’ 好于 A (都是正向的), B 是随机, C 是一个反效果 (跟 C’ 沿红线轴对称, 就是说把 C 的结果反过来就得到 C’).

如果我们有足够多的样本, 则对一个分类器可以在 ROC 曲线图上画出若干个点, 把这些点和 (0, 0), (1, 1) 连起来求凸包, 就得到了 AUC 面积 (Area Under Curve, 曲线下面积). 非常明显, 这个凸包的最小下面积是 0.5 (从 (0, 0) 到 (1, 1) 的这条线), 最大是 1.0 (整个矩形面积), AUC 值越大, 说明分类效果越好.

用 ROC 曲线定义的方式来描点计算面积会很麻烦, 不过还好前人给了我们一个近似公式, 我找到的最原始出处是 Hand, Till 在 Machine Learning 2001 上的一篇文章给出 [文章链接]. 中间的推导过程比较繁琐, 直接说我对这个计算方法的理解: 将所有样本按预估概率从小到大排序, 然后从 (0, 0) 点开始描点, 每个新的点是在前一个点的基础上, 横坐标加上当前样本的正例在总正例数中的占比, 纵坐标加上当前样本的负例在总负例数中的占比, 最终的终点一定是 (1, 1), 对这个曲线求面积, 即得到 AUC. 其物理意义也非常直观, 如果我们把负例都排在正例前面, 则曲线一定是先往上再往右, 得到的面积大于 0.5, 说明分类器效果比随机好, 最极端的情况就是所有负例都在正例前, 则曲线就是 (0, 0) -> (0, 1) -> (1, 1) 这样的形状, 面积为 1.0.

同样给一份 C 代码实现:

struct SampleNode {
  double predict_value;
  unsigned int pos_num;
  unsigned int neg_num;
};

int cmp(const void *a, const void *b)
{
   SampleNode *aa = (SampleNode *)a;
   SampleNode *bb = (SampleNode *)b;
   return(((aa->predict_value)-(bb->predict_value)>0)?1:-1);
}

double calcAuc(SampleNode samples[], int sample_num) {
  qsort(samples, sample_num, sizeof(SampleNode), cmp);

  // init all counters
  double sum_pos = 0;
  double sum_neg = 0;
  double new_neg = 0;
  double rp = 0;
  for (int i = 0; i < sample_num; ++i) {
    if (samples[i].neg_num >= 0) {
      new_neg += samples[i].neg_num;
    }

    if (samples[i].pos_num >= 0) {
      // calc as trapezium, not rectangle
      rp += samples[i].pos_num * (sum_neg + new_neg)/2;
      sum_pos += samples[i].pos_num;
    }
    sum_neg = new_neg;
  }

  return rp/(sum_pos*sum_neg);
}

分类器的一致性

如果分类器的概率结果就是最终结果序, 那 AUC 值基本可以当作最终效果来用. 但是实际应用中分类器的结果都要再做函数转换才是最终序, 则评估的时候需要将转换函数也带上去做 AUC 评估才行. 某些应用中这个转换函数是不确定的, 比如广告的价格随时会变, 推荐条目的重要性或收益可能也是另一个计算模型的结果. 在这种情况下, 如果我们可以保证分类器概率和实际概率一致, 让后续的转换函数拿到一个正确的输入, 那么在实际应用中才能达到最优性能.

为了评估分类器概率和实际概率的一致性, 引入 MAE (Mean Absolute Error, 平均绝对误差) 这个指标, 维基百科对应的词条是 Mean_absolute_error. 最终的计算方法很简单, 对样本 i, f_i 是预估概率, y_i 是实际概率, 则 i 上绝对误差是 e_i, 累加求平均就是 MAE:

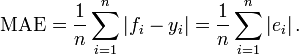
MAE 的值域是 [0, +∞), 值越小说明分类器输出和实际值的一致性越好. 我个人认为如果 MAE 和实际概率一样大, 那这个分类器的波动效果也大到让预估近似随机了.

MAE 看起来和标准差有点像, 类似标准差和方差的关系, MAE 也有一个对应的 MSE (Mean Squared Error, 均方差?), 这个指标更多考虑的是极坏情况的影响, 计算比较麻烦, 一般用的也不多, 有兴趣的可以看维基百科上的词条 Mean_squared_error.

MAE 计算太简单, MSE 计算太纠结, 所以都不在这给出代码实现.