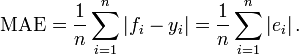距离 2012 的两三年后(这篇的草稿时间)又过了两三年,这个补遗看起来也烂尾了 -.-
之前在机器学习手记系列 3: 线性回归和最小二乘法后面留了个问题, 也给了结果, 但是当时说好的程序代码并没给出来, 那个手记系列的坑感觉填不上了, 但是已经刨好的小坑还是填上吧
现在已经有很多深度学习框架和教程来教这个,自己也忘得差不多了,就不班门弄斧裸写。推荐看一下 动手学深度学习 http://zh.gluon.ai/index.html,Deep Learning 领域大神 李沐 等人在维护(我能凑不要脸的蹭热度说下这是前百度同事我们还一起吃饭打牌来着么)。刨的小坑就按 线性回归的从零开始实现 http://zh.gluon.ai/chapter_deep-learning-basics/linear-regression-scratch.html 里的做法来实现
先重复下问题
如下式子里不同的阿拉伯数字只是一个符号, 实际表示的可能是其他数字
967621 = 3
797321 = 1
378581 = 4
422151 = 0
535951 = 1
335771 = 0根据上述式子, 判断下式等于?
565441 = ?
这题的脑筋急转弯版本答案是看每个数字有几个圈,就代表几,这样 1/2/3/4/5/7 都是 0 个圈,6/9 是 1 个圈,8 是 2 个圈,所以最后 565441 里面只有 6 有 1 个圈,答案为 1
按 gluon 上的教程我们也来走一遍,装环境什么的就看 gluon 了,先引入要用的包
from mxnet import autograd, nd
真正做线性回归是没法只用这么一点数据来模拟的,所以我们要先根据真实值来构造一些数据(这里跟 gluon 不一样的是我没有 bias 因子 b,后面也请一并注意)
num_inputs = 9 # 特征数,当前问题里的变量数 1-9 num_examples = 1000 # 样例数,我们会随机生成多少份样例来学习 true_w = nd.array([0, 0, 0, 0, 0, 1, 0, 2, 1]) # 真实值 features = nd.random.normal(scale=1, shape=(num_examples, num_inputs)) # 随机生成数据集 labels = nd.dot(features, true_w) # 数据集对应的结果
初始化模型参数并创建梯度
w = nd.random.normal(scale=0.01, shape=(9, 1)) w.attach_grad()
定义模型,我们就是做的矩阵乘法
def linreg(X, w):
return nd.dot(X, w)
定义损失函数,用平方损失
def squared_loss(y_hat, y):
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
定义优化算法,用小批量随机梯度下降(因为我们只用了一个大参数 w,所以还是比 gluon 的样例简单)
def sgd(param, lr, batch_size):
param[:] = param - lr * param.grad / batch_size
训练,取步长 lr 为 0.01,轮次为 1000 轮
def train():
lr = 0.01
num_epochs = 1000
net = linreg
loss = squared_loss
for epoch in range(num_epochs):
with autograd.record():
l = loss(net(features, w), labels)
l.backward()
sgd(w, lr, labels.size)
train_l = loss(net(features, w), labels)
if epoch % 100 == 99:
print("epoch {}, loss {}, w {}".format(epoch + 1, train_l.mean().asnumpy(), w))
验证下结果看看
if __name__ == "__main__":
train()
test = nd.array([1, 0, 0, 2, 2, 1, 0, 0, 0]) # 测试集,565441
print(nd.dot(test, w))
随便跑了一次输出如下,注意模型里每个值的科学计数法的指数
epoch 1000, loss [ 5.72006487e-09], w [[ -6.20802666e-06] [ 1.62000088e-05] [ -1.03610901e-05] [ 7.82768348e-06] [ 2.59973749e-05] [ 9.99964714e-01] [ 1.86312645e-05] [ 1.99990368e+00] [ 1.00001490e+00]] <NDArray 9x1 @cpu(0)> [ 1.00002611] <NDArray 1 @cpu(0)>
忽略精度问题,可以认为符合真实结果
全部代码详见 https://gist.github.com/whusnoopy/af0aa6fd276ace8a7c4d483e586e936d