系列说明
按合总指示, 给人人的机器学习小组写点科普性质的东西. 其实自己好像一直都没去系统的学过这些东西, 都是野路子乱搞, 这里把过去学的一点东西写出来, 记录一下, 班门弄斧, 欢迎拍砖.
自己接触到的机器学习, 几乎都是在用历史预估未来某事件发生的概率 (广告点击率, 推荐接受度, 等等).
将这个过程细化一下, 首先都是对历史样本提取特征, 将样本转换成用特征序列来描述, 将同类事件合并, 然后通过某种拟合方式去让特征带上合适的权重, 用于描述事件发生的概率, 最后对还未发生的同类事件, 同样将其转换成特征序列, 用学出来的权重转换成预估概率.
这里有两个关键问题, 一是特征选取, 二是拟合还原方法. 特征选取是为了将样本做合理拆分合并, 同质的才划分到一起, 不然就最后的预估还是随机猜. 拟合还原方法是保证在对数据做了合理拆分后, 能将特征的权重拟合到原数据上且能在预估时还原成概率.
问题
对怎么选特征, 似乎从来都没有好的普适性方法, 但是怎么验证选的特征靠不靠谱, 方法倒是挺多. 先抛开选特征的指导方向不说 (说也说不清), 如果我们选出了一类描述特征, 怎么验证其效果?
特征效果验证
最直接粗暴也是终极方案就是直接拿到线上去应用, 好就是好, 不好就是不好. 这是一句彻底的废话, 也是真理… 不过实际操作中很难真的去这么做, 一是如果要完成整个流程会比较耗时和麻烦, 二是没有那么多线上资源拿来实验, 三是如果实验不好带来的负面影响会非常大, 广告会损失收入, 推荐会严重影响用户体验. 所以如果线下没验证的心里有谱, 没人敢直接拍上去实验的, 老板也不会让乱来, 都是钱和能转换成钱的用户啊.
退回到离线验证上, 终极离线验证也还是拿机器学习的产出 (分类树, LR 模型, 或别的什么) 去评估一部分实验数据, 然后看对实验数据的预估结果是否和实验数据的实际表现一致. 这个还是存在耗时耗资源的问题, 后面再说, 先说简单的.
不管是分类树, 还是 LR 或别的 boosting 什么的, 都是希望能找到有区分度的特征, 能将未来不同的数据尽可能划开. 如果特征是一个 0/1 特征, 那数据就应该能明显被分成不一样的两份. 比如在豆瓣, “历史上关注过计算机类别书目的人” 是一个 0/1 特征, 如果拿这个特征来分拆人群, 并评估 “未来是否关注计算机类别书目”, 评估指标的 1 绝大部分都落在区分特征的 1 中, 那说明这是一个非常正相关的区分 (曾经干过某事的人会继续干另一件事), 效果很好, 反之拿去评估 “未来是否关注女性言情小说类别书目”, 很可能评估指标的 1 绝大部分都落在区分特征的 0 里, 那是非常负相关的区分 (曾经干过某事的人不会再干另一件特定的事), 效果也挺好, 但是如果是评估 “未来是否会关注武侠”, 评估指标的 1 是比较均匀的散布在区分特征的 0/1 里, 那就说明这个特征对该评估指标没有区分度, 还不如没有. (这些例子是随便拍脑袋写的, 不保证其正确性)
如果是一维连续特征, 则最后总特征总可以转换成一个一维向量 (连续值可以离散化成整数区间), 跟 0/1 特征一样, 比较这个特征的自变量取值向量和对应到评估数据上的取值向量的相关度就能判断效果好坏 (正相关或负相关都是好的). 一般最简单的是使用 Pearson (皮尔生) 乘积矩相关系数 r 来做是否线性相关的判断, 英文 wiki 上的条目 Pearson product-moment correlation coefficient 对该系数的含义和计算方法有比较详细的说明, 中文翻译比较杂, 百度百科上的是皮尔森相关系数, 微软的翻译是皮尔生相似度. 简要的说, pearson 相关系数是一个 [-1, 1] 之间的实数, 取值越接近 -1 表示特征值和评估值越负线性相关, 越接近 1 表示越正相关, 越接近 0 表示越不相关 (只是线性, 可能会有其他相关的关系).
还是拿豆瓣的例子说, 比如 “历史上关注过计算机类别书的数量” 作为一个人群划分特征, 那这维特征的自变量向量会是 <0, 1, 2, ...>, 为了取值方便, 将其截断到超过十本的也等于 10, 则向量变为 <0, 1, ..., 10>, 如果去评估 “继续关注计算机类别书的概率”, 这个概率取值可能是 <0.0, 0.1, ..., 1.0>, 则其 Pearson 相似度会是 1. (当然, 这个例子举的太假了点, 先这么着吧)
将问题化简为算特征取值和评估指标的 Pearson 相似度后需要做的工作就会少很多, 直接跑个 Map/Reduce 从 LOG 里提取下数据, 然后看看值的相关性就知道特征是否有区分度了, 没区分度的可以先不考虑 (或者将曲线相关的可能转变成线性关系, 再判断), 有区分度的才继续走更完整的离线验证, 加入分类树或概率模型和其他特征一起作用看效果, 如果还不错就上线实验.
微软的 Excel 里就带了 Pearson 相似度的计算公式, 可以很方便的拿来评估, 说明和用法请见微软帮助页面 PEARSON 函数. 如果要自己计算, 可以参考 wiki 的这个公式:
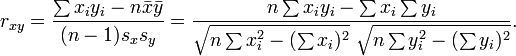
C 的实现源码如下 (注意某些情况下可能会有计算精度丢失, 带来结果的不确定性)
double pearson_r(double x[], int x_n, double y[], int y_n) {
if (x_n != y_n || x_n == 0) {
return 0;
}
double n = (double)(x_n);
double sum_x = 0;
double sum_y = 0;
double sum_x_sq = 0;
double sum_y_sq = 0;
double sum_x_by_y = 0;
for (int i = 0; i < x_n; ++i) {
sum_x += x[i];
sum_y += y[i];
sum_x_sq += x[i]*x[i];
sum_y_sq += y[i]*y[i];
sum_x_by_y += x[i]*y[i];
}
double res = n*sum_x_by_y - sum_x*sum_y;
res /= sqrt(n*sum_x_sq - sum_x*sum_x);
res /= sqrt(n*sum_y_sq - sum_y*sum_y);
return res;
}